결정론적 확률과 확률론적 확률과 강화학습의 확률

확률(probability)은 AI 분야에서 처음부터 끝까지 함께 붙어 다니는 개념이다.
어찌보면 단순한 것이지만, 본질적으로 물리학적인 관점으로 살펴보면 재미있고도 중요한 것을 느낄 수 있다. 몇 가지 대표적인 확률을 들어 정리해 본다.
▶결정론적 확률 (probability of deterministic)
힘의 원리를 발견한 뉴턴(Newton)의 고전 역학에서 유래한 결정론적 세계관은 신의 영역으로 여겨졌던 미래의 예측에서 신을 완전히 배제하고 간단한 수식만으로 미래의 상태를 매우 잘 예측하며 천체 예측이나 교량 건축 등에서 인류의 지성을 크게 성장시켰다.
사과 나무 가지에서 사과의 꼭지가 분리되면, 사과는 좌우나 위로 움직이지 않고 아래로 반드시 떨어진다. 사과가 바닥으로 떨어지지 않을 확률은 언제나 0이다.
과거에 복권 추첨은 회전하는 피자 모양 원판과 화살을 사용하여 무작위(?)성을 부여하여 추첨을 하였다. 그러나, 화살 추첨 방식은 뉴턴의 힘의 역학에 따라서 움직이는 것이 명백하다.
즉, 미래에 화살이 꽂힐 1등의 숫자는 화살이 회전판에 꽂히기 전에 화살의 발사 시점에서 이미 미래를 정확히 예측할 수 있는 것으로서 엄밀히 보면 무작위가 아니다. 회전판과 화살의 속도와 초기값만 알면, 미래의 숫자를 정확히 미리 알 수 있다. 그러나, 얼추 편의상 무작위성의 확률 개념을 부여하여 사용하고 있다.

과거의 재미있는 뉴스에 의하면, 미국 공대 대학원생이 휴대용 컴퓨터를 이용하여 카지노의 룰렛의 초기 상태와 쇠구슬과 회전판의 속도를 컴퓨터로 계산하여 돈을 따서 수상히 여긴 카지노 측에 발각되어 쫓겨난 뉴스가 있었다.
완전한 확률 시스템인 듯한 카지노의 룰렛 시스템도 물리학적 변수의 완전한 수치를 알면 미래가 즉시 결정된다. 완전한 정확한 수치를 모르고 약간의 오차가 있으면 미래의 상태 예측에 오차가 발생하기에 이 부분에 확률이 적용되어 좀 더 합리적인 예측을 한다.

▶결정론적 카오스 확률 (probability of chaos)
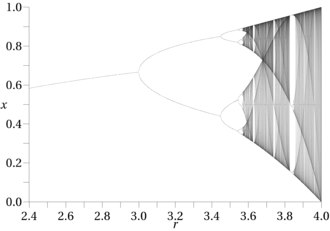
풀이 자라나는 속도와 풀을 먹고 사는 토끼의 번식에 의한 개체수는 카오스 시스템이다. 토끼 번식률에 따라서 미래 토끼의 개체수는 정확한 수식으로 명백하게 나타낼 수 있지만, 토끼 번식률 측정의 미세한 오차로 인하여 미래의 예측은 매우 크게 벗어난다. 토끼의 개체수는 2중 분기 (bifurcation)에 의해서 급격히 복잡해지는 그래프를 볼 수 있다.
이러한 다른 예는 매우 잘 알려져있는 것으로 난류와 기상 현상이 있다. 난류와 기상 현상은 명백한 완벽한 방정식인 나비에 스톡스 방정식 (Navier-Stokes equation)을 정확히 따른다. 명백한 방정식이 있지만 완벽한 측정값은 불가능하기에 미래는 확률적으로나 가까스로 접근하는 것이다.
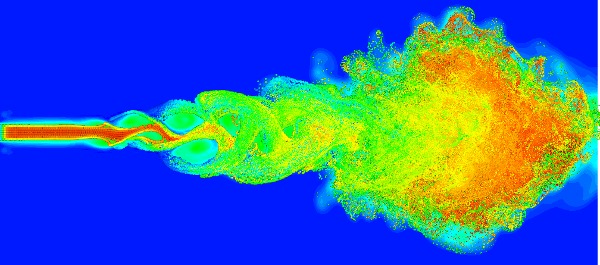
이러한 결정론적 카오스는 비선형성(non-linearity) 때문에 변화무쌍하게 나타나는 것이다.
딥러닝 AI에서 가장 널리 사용하는 활성화함수(activation function)인 ReLU (Rectified Linear Unit)은 비선형성때문에 좋은 성능을 내는 활성화함수가 된다.
▶확률론적 확률 (probability of stochastic)
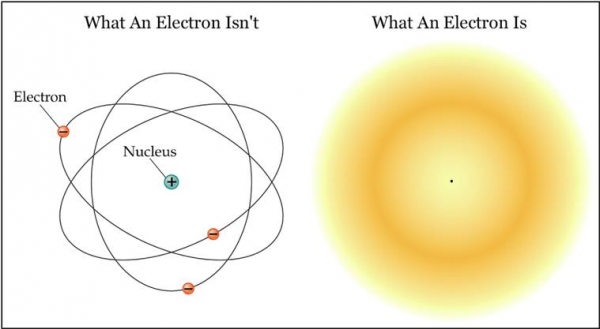
확률론적 확률의 가장 정확한 예로는 원자 속에 있는 전자의 위치에 대한 것으로 볼 수 있다. 전자의 실제 위치를 정확히 모르기 때문에 확률로 접근하는 것이 아니라, 전자 자체가 실제로 확률적으로 모든 공간에 실재로 분포하기 때문이다. 측정하는 방식에 따라서 여러 위치에 하나의 전자가 동시에 실재로 위치하여 1개의 전자가 서로 간섭도 한다. 이러한 사실은 중첩이라고 부르며 양자 컴퓨터의 기본 원리가 된다.
정확히 결정되어 있는 것을 잘 모르는 경우에 어쩔 수 없이 접근하기 위한 근사적인 방법으로써 확률을 다루는 것이 아니라 실재로 물리학적으로 확률론적으로 존재하는 진정한 확률론적 확률이라고 할 수 있다.
▶확률적 관측과 확률적 행동
현실세계에서의 강화학습의 경우에는 환경에 대한 모든 것을 알 수 없으며 일부만을 확률적으로만 알 수 있는 경우가 있다. 이러한 경우에 재미있는 사실은 확률적으로만 알 수 있는 환경에서 agent의 action은 deterministic 하게 action을 취하는 것보다 stochastic 하게 action을 취하는 것이 더 좋은 결과를 내는 것은 흥미로운 사실이라고 할 수 있다.

