여러분야에서 딥러닝이 사용되는 내적의 의미와 실제 사용에 관하여

본고에서는 인공지능(AI)의 여러분야에서 사용되는 딥러닝의 내적 의미와 실제 사용에 관하여 알아본다.
▷인공신경망 벡터의 내적(dot product)은 인공신경망의 각 뉴런 노드의 입력과 가중치 (weight)의 상호관계의 계산에 사용된다.
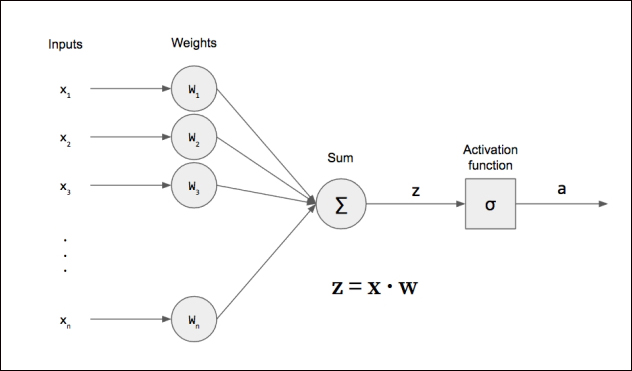
각 입력값에 가중치를 곱하여 전체를 더하는 것이 입문자가 받아들이는 방식이라면, 입력값 전체를 여러개의 축(axis)을 가진 하나의 벡터(vector)값으로 보고, 가중치 전체를 여러개의 축을 가진 하나의 벡터값으로 보아, 단지 input vector와 weight vector 2개의 벡터의 dot product 라고 보면, 아무리 입력값이 많아져도 아주 간단하게 전체를 단순화하여 인식할 수 있게 된다.
▷ 내적의 물리적 의미
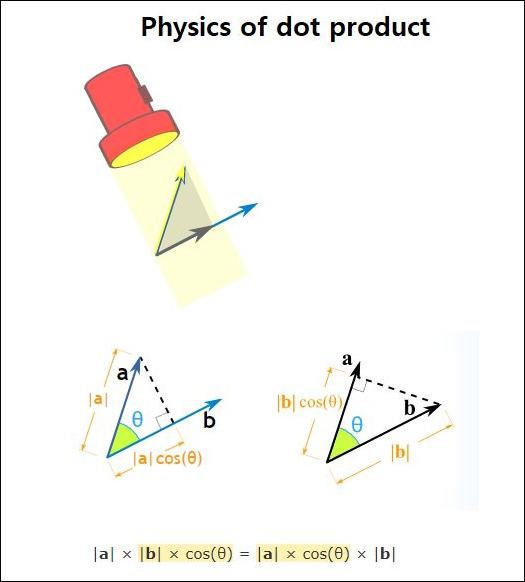
인공신경망에서 벡터의 내적(dot product) 계산은 기본적으로 많이 사용된다. 추상적인 내용을 현실적으로 받아들이기 위해서 벡터의 내적에 대한 물리학적인 의미를 알아보는 것이 도움이 된다.
힘(force)은 방향과 크기가 있는 벡터이다. 서로 다른 방향으로 작용하는 2개의 힘(벡터)이 있을 때, 서로 상호협력하여 얼마나 효과를 내는지가 벡터의 내적이라고 할 수 있다.
벡터는 서로 같은 방향에 대한 성분에 대해서만 실질적으로 영향을 명시적으로 알 수 있어서, 같은 방향으로 작용하는 힘에 대해서 알아내야 한다.
그림의 a 벡터를 b 벡터에 수직으로 빛을 비추면, b벡터에 a 벡터의 그림자가 나타나는데, a 벡터의 그림자의 길이는 b 벡터와 협력하는 a 벡터의 크기라고 할 수 있다.
이제 같은 방향을 가지는 벡터가 되었으므로, a 벡터 그림자의 크기와 b 벡터의 길이를 곱한 값이 내적 값이 된다.
b 벡터에 수직으로 빛을 비추어 a 벡터의 그림자를 이용하여 계산한 내적 값이나, 반대로 a 벡터에 수직으로 빛을 비추어 b 벡터의 그림자를 이용하여 계산한 내적 값은 같다.
이러한 개념을 확장하여 신경망에 대입해 보자.
입력값과 가중치를 내적한 값을 이용하는데, 이것은 입력값 벡터 a 와 가중치 벡터 b 를 서로 같은 방향으로 (빛을 수직으로 비추어 그림자 길이 이용) 맞춘 후 길이를 서로 곱한 것으로 생각할 수 있다.
결과적으로, 입력 벡터와 가중치 벡터의 상호협력하여 얼마나 효과를 내는지 그 크기를 활성화 함수 (ReLU)로 넣어주는 의미로 추상화할 수 있다.
▷코사인 유사도 (Cosine Similarity)
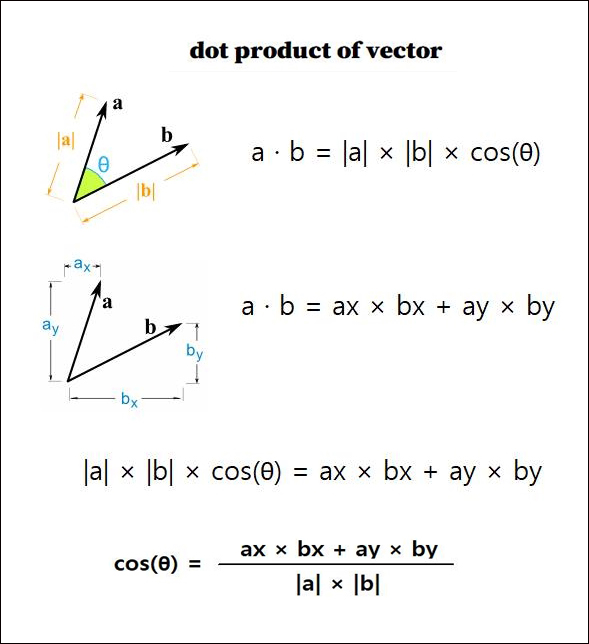
2개 벡터의 내적 값은 cos (각도)를 이용한 값이나 직교좌표의 성분으로 구한 값이나 하나의 수치값 (scalar)으로 같다. 딥러닝에서의 벡터는 각 특성(feature)이 축(axis)에 해당되어서, 모든 feature 는 직교좌표 개념으로 표현된다.
그래서, 두 벡터에 대해서 직교좌표에서 구한 내적과 벡터의 길이값으로 cos(각도) 값을 구할 수 있음을 뜻한다. 두 벡터의 각도가 0도에 가까우면 거의 같은 종류의 특성 벡터임을 의미하고, 각도가 90도가 되면 전혀 상관없는 특성 벡터임을 의미한다.
일반적인 거리 (유클리드 거리)에 의한 분류는, 문서에서 각 단어의 등장횟수만 다르고 분포가 같다면,거리가 많이 떨어지게 되어 다른 종류의 문서로 분류하지만, 각도에 의한 거리로 재면 서로 비슷한 방향의 벡터로서 각도 거리는 가깝게 되어 같은 종류의 문서로 분류할 수 있다.
각도를 사용하여 유사한 정도를 재는 이러한 방식을 코사인 유사도 (cosine similarity) 라고 부른다.
▷내적 유사도 (Dot Product Similarity)
코사인 유사도보다 더 간단한 유사도를 구하는 방법에 대해서 알아보자.
각 문서 A B C에서 특정 4개 단어의 빈도수를 벡터로 표기하자.
A= [1,1,0,0] B= [0,0,1,1], C= [0,1,1,1]
simDot(A,B)= 1x0+1x0+0x1+0x1= 0, simDot(A,C)= 1x0+1x1+0x1+0x1= 1, simDot(B,C)= 0x0+0x1+1x1+1x1= 2
4개 feature axis (축)을 가지는 벡터 공간에서, A 문서는 앞부분 2개 특성을 가지고 있고, B 문서는 뒷부분 2개 특성을 가지고 있고, C 문서는 뒷부분 3개 특성을 가지고 있다.
사람이 그냥 딱 보기에도, A 와 B 는 전혀 같은 특성이 없는 별개의 문서이고, A 와 C 는 두번째 특성 1개만 동시에 가지고 있다. B 와 C 는 뒷쪽 특성 2개를 동시에 가지고 있다.
그러므로, 가장 비슷한 문서는 A, C이고, 가장 다른 문서는 A, B이다. 이렇듯, 벡터의 간단한 dot product 자체만으로도 벡터간의 유사한 정도를 계산할 수 있다.
그러나, A 의 2번째 특성의 크기를 10이라면,
A= [1,10,0,0], B= [0, 0,1,1], C= [0, 1,1,1]
simDot (A,C)= 1x0+10x1+0x1+0x1= 10이 되어서 A C 문서가 가장 가깝다는 계산이 나오는 특성이 있다.
각각의 벡터의 길이가 비슷한 경우라면, 벡터의 내적만으로도 유사도를 쉽게 구할 수 있다. 벡터의 내적의 계산법만이 중요한 것이 아니라, 적용되는 곳에 따라서 그 내부의 본질적인 의미를 아는 것은 중요하다.
이러한 관점은 물리학에서 나타나는 수식 자체보다도, 그 수식이 나타내는 본질적인 의미를 깨닫는 것이 중요하다는 것과도 일맥상통하는 관점이다.
▷어텐션 메카니즘의 내적 유사도(Dot Product Similarity of Attention Mechanism)
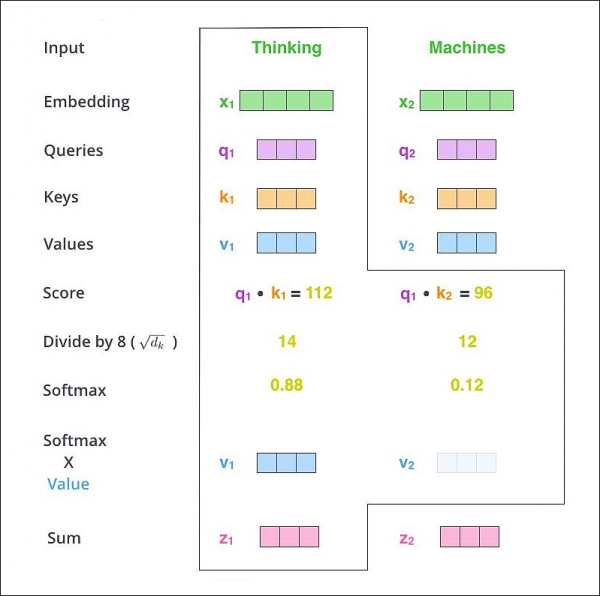
두 벡터의 내적이 두 벡터의 비슷한 정도를 나타낼 수 있음을 앞서 살펴보았다. 최근 가장 좋은 성능을 내고 있는 Attention 에서 내적 유사도가 사용되고 있다.
Attention은 Keys Values가 준비된 상태에서 Query에 대하여 적절한 Value를 얻는 것이 목적이다.
Value를 얻기 위해서는 Query와 비슷한 Key를 찾아야 하는데, Query 벡터와 비슷한 Key 벡터를 찾는 방법으로 Query와 Key의 비슷한 정도의 score를 Query 벡터와 Key 벡터의 dot product를 이용하여 비슷한 정도를 계산하는데 사용한다.
이와 같이, 이러한 내부적인 의미는 계산 방법만에 촛점을 맞추어서는 전체적인 깊은 의미를 파악하기 어렵게 된다. 벡터의 내적은 같은 계산법이지만, 각기 다른 내부적인 의미를 가지는 가에 따라서 다른 목적으로 다양하게 의미가 크게 사용되고 있다.

