RNN 방식은 전체 입력값을 한번에 같이 입력할 수 없는 단점이 존재하고, 순차적으로만 입력해야 하기에 많은 계산 시간이 소요되며, GPU의 병렬 처리를 효율적으로 이용할 수 없는 구조를 가진다.

최근 인공지능(AI) 기술분야에는 워낙 많은 개념과 모델이 하루가 다르게 대두되다 보니, 전체적인 개념 이해가 어려운게 사실이다. 본고에서는 일반인의 관점에서 트랜스포머 어텐션(Transformer Attention)에서 사용하는 위치 엔코딩(Positional Encoding)에 대해서 알아 본다.
▷ 순환신경망(Recurrent Neural Network 이하, RNN)에서의 순서 위치 정보
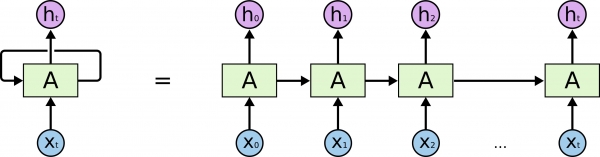
RNN에서는 입력값이 입력되는 순서에 대한 정보는 앞선 출력값이 새로운 입력값과 함께 다시 입력되는 과정에서 자연스럽게 순서 위치에 대한 정보도 함께 고려되어서 처리된다.
이러한 이유로 RNN에서는 입력값이 입력되는 과정에서 굳이 명시적으로 현재 Time Step의 입력값이 전체 순서에서 몇 번째 입력값으로서 입력되는지 정보를 줄 필요가 없이 저절로 처리된다.
그러나, RNN 방식은 전체 입력값을 한번에 같이 입력할 수 없는 단점이 존재하고, 순차적으로만 입력해야 하기에 많은 계산 시간이 소요되며, GPU의 병렬 처리를 효율적으로 이용할 수 없는 구조를 가진다.
▷ 원핫 엔코딩(One-Hot Encoding)
원핫 엔코딩을 이용한 위치 엔코딩 방식은 전체의 순서 위치에 대해서 유일한 하나의 위치 값을 줄 수는 있다. 하지만, 원핫 엔코딩은 본질적으로 단순히 유일한 값만을 배당하는 목적으로 사용하는 것일 뿐이므로, 입력값의 상호 순서간의 상관성을 가지게 하는데는 한계가 있다.
또한, 원핫 엔코딩은 절대적인 위치의 정보를 이용하는 방식보다는 상호간의 상대적인 위치 정보를 이용해야만 좋은 결과를 얻을 수 있다.
▷ 사인(Sine) 함수의 이용
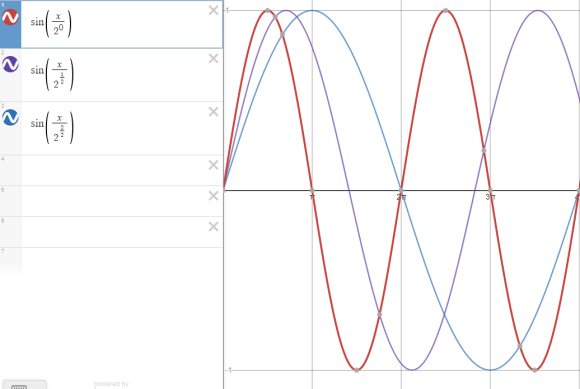
사인 함수를 이용하면, 각각의 위치 (x) 에 대한 상호간의 관계를 부드럽게 연결해 줄 수 있다.
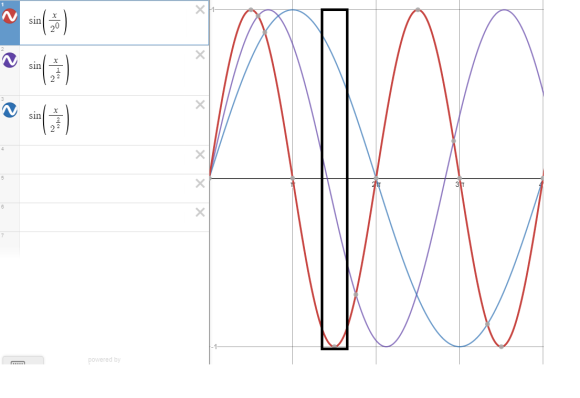
또한, 하나의 사인 함수를 사용하면 서로 다른 위치에서 동일한 Sin(x)값을 가질 수가 있지만, 서로 다른 주기의 Sine 함수를 조합하면 각 위치에서 모두 다른 유일한 값을 가지게할 수 있으며, 이러한 방식을 정현파 위치 인코딩(Sinusoidal Positional Encoding) 이라고 한다.
코사인(Cosine) 함수는 사인 함수를 옆으로 이동시킨(Shift) 것이므로 동일하게 Sinusoidal 부류로 취급할 수 있다. 하나의 위치에 대해서, 서로 다른 주기 (주파수)의 sin(x), cos(x) 여러개의 수치를 모아서 위치를 표현하는 수열 (Encoding)로 표현할 수 있다.
아래의 그림은 각각의 위치에 대하여 정현파 위치 인코딩 값을 보기 쉽게 표시한 것이다. 세로축 (y축)은 위로부터 아래 방향으로 위치 (Position)을 표시한 것이고, 가로축 (x축)은 Positional Encoding을 표현한 것으로서, 왼쪽은 Sin(x) 값을 색으로 표현하고 오른쪽은 Cos(x)값을 색으로 표현한 것이다.
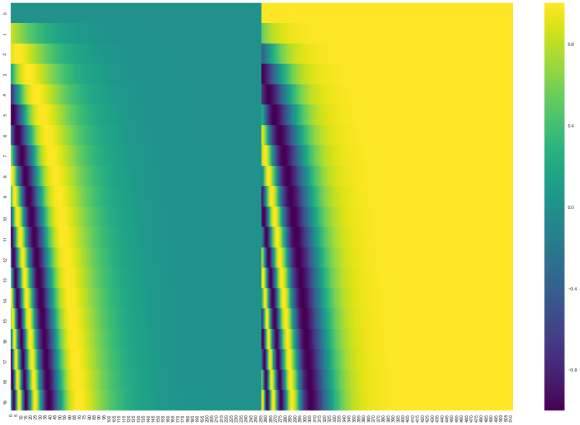
세로축 위로부터 index = 5 위치의 왼쪽만 떼어서 보면 더 쉽게 이해할 수 있다.

Position 5 하나의 위치에 대해서, 여러가지 주기 (주파수)에 대한 Sine 함수의 값을 표현하고 있다. 왼쪽은 주기가 짧은 즉, 주파수가 높아서 빨리 변하는 Sine 함수이고, 오른쪽은 주기가 길어서 즉, 주파수가 낮아서 늦게 변하는 Sine 함수 영역이다.
가장 왼쪽은 빨리 변하는 sin (x) 라서 0으로 시작한 sin (x)가 -1 (남색) 바닥까지 내려온 상태이고, 약간 오른쪽 (주파수가 약간 길어진)은 0 으로 시작한 Sine 그래프가 이제 비로서 최고 정점인 1 (노랑)까지 올라간 것이다.
더 오른쪽은 주기가 길고 주파수가 낮아서, 0에서 시작한 Sine 그래프가 Position 5까지 왔음에도 아직 녹색으로서 Sine 시작값인 0 근처에 있음을 뜻한다.
가장 왼쪽만 세로로 길게 그림을 자르면 아래와 같이 되는데, 가장 주기가 짧고 주파수가 큰 Sine 함수가 위치가 커짐에 따라서 (세로로 이동하면서) Sine 함수의 시작값인 0 (녹색)에서 시작해서 최고값인 +1 (노랑)을 지나서 0값 (녹색)을 지나고, 최소값인 -1 (남색)이 되는 과정을 반복함을 알 수 있다.


Attention의 Transformer 에서 사용하는 Positional Encoding 은 하나의 위치에 대해서 Positional Encoding 값 수열을 짝수는 Sine 함수를 사용하고, 홀수는 Cosine 함수를 사용한다.
그래서, 첫째 세로칸은 Sine의 시작값인 0으로 시작 (녹색)하고 +1 (노랑) 으로 색이 변하고 있고, 둘째 세로칸은 Cosine 시작값인 +1 로 시작 (노랑)하고 0 (녹색)으로 색이 변하고 있다.
▷ Sin, Cos 섞어서 사용하는 이유
Sine 함수만을 사용하지 않고, Cosine 함수를 섞어서 사용하는 이유는 다음과 같다.
Cosine 함수는 단지 Sine 함수를 옆으로 밀어서 이동시킨 Sine 함수에 불과하기도 하고, 위치간의 상호 상대적인 상호 관계가 내부적으로는 행렬의 회전변환에 의해서 상호 변환될 수 있는 관계가 있기 때문이다.
행렬의 회전변환은 Sine Cosine 함수로 이루어져 있다.
▷ Concatenation 을 사용하지 않고 Adding을 사용하는 이유
입력되는 WE (word embedding)의 차원이 큰 경우에는 Concatenation을 위해서는 PE (position encoding) 도 같은 크기의 메모리를 필요로하게 되어서, 큰 메모리 용량을 필요로 하게 되며 입력값의 차원이 커지게 되면, Self-Attention 계산에서 급격히 파리머터 갯수가 증가하게 된다.
Concatenation 대신에 단순히 수치를 Adding을 하게 되면, Positional Encoding 정보를 더했지만, 원래 입력값의 차원을 유지하게 되어서, 내부적으로 처리될 Self-Attention 의 계산을 크게 간소화시킬 수 있다.
마지막으로 ▷WE (word embedding)과 PE (position encoding)을 곱셈하지 않고 덧셈을 하는 이유는, 곱셈을 하면 PE의 수열에서 0인 부분이 있다면, 중요한 정보인 WE의 정보를 없애버릴 수 있기 때문으로, 곱셈보다 덧셈을 하면 중요한 정보인 WE의 정보를 유지하면서 위치 정보를 덧씌울 수 있기 때문이다.

